



WHAT WAS LOST
Tracing unmet demand in contraceptive supply chains
Harsha Halgamuwe Hewage
Data Lab for Social Good Research Group, Cardiff University, UK
Lead Supervisor: Prof. Bahman Rostami-Tabar
Co Supervisors: Prof. Aris Syntetos & Dr. Federico Liberatore
2025-06-24
Outline

What was never COUNTED . . .
The fundamental question
What we are going to do
Numerical experiment
What’s NEXT
WHAT WAS NEVER COUNTED…
Seen the UNSEEN
Human story: What data misses

Nilu went to a pharmacy for Product A.
It was not in stock and the system logs it as
zero demand.
This creates broken trust and leads to create
UNMET DEMAND.
Seen the UNSEEN
Analytical reality: Why this matters

Stockouts censor demand.
Observed sales ≠ actual demand.
Inventory decisions based on this false signal?
Understocking → more stockouts.
Forecasts don’t just underperform. They miss the whole story.
A lost sale = a lost opportunity for care.
Contraceptive products aren’t easily SUBSTITUTED
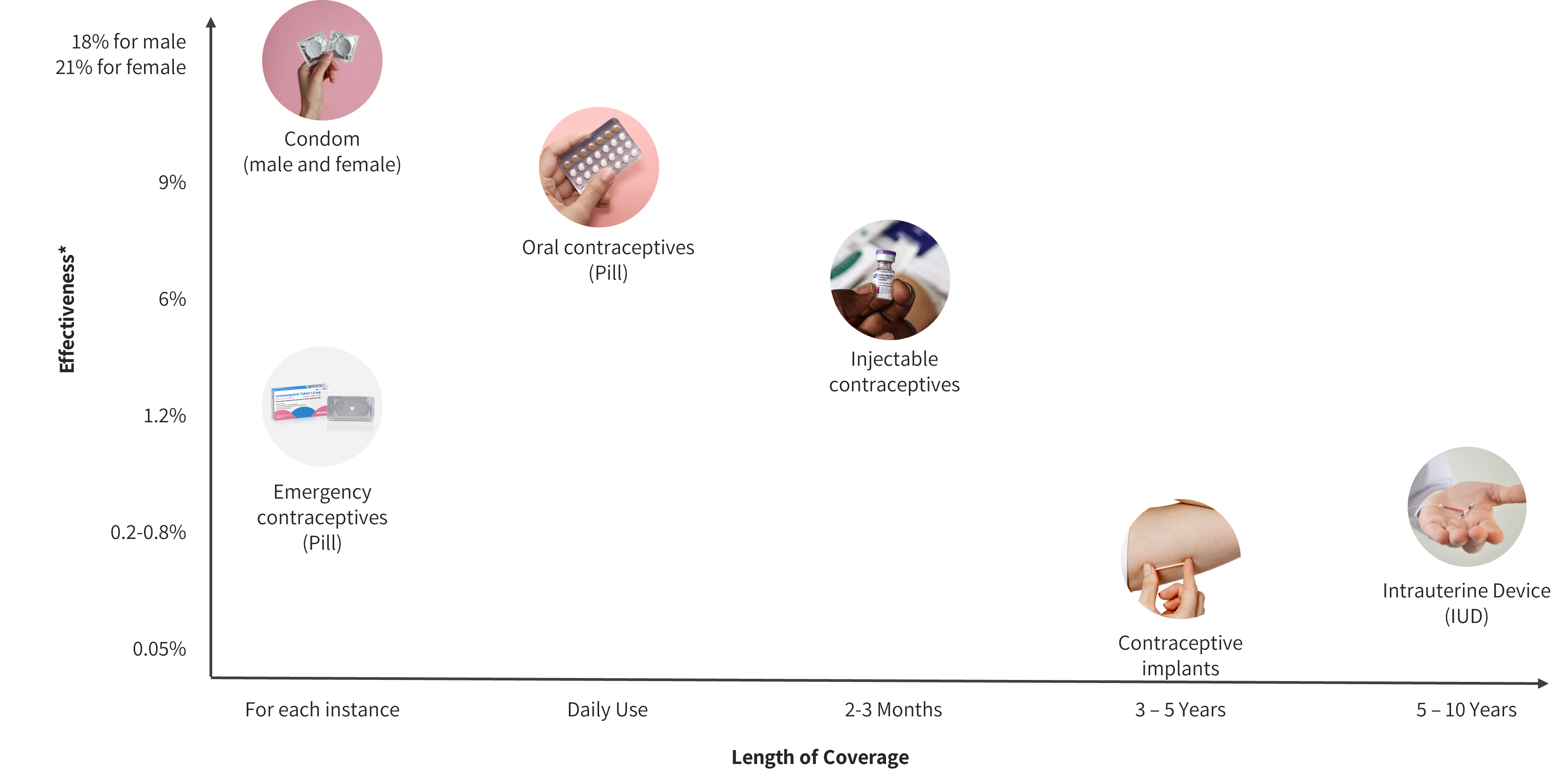
The BIG PICTURE

In reality…
There are more than
218 million women
like Nilu still have an unmet need for family planning.
Ultimately, this results in dropouts, unwanted pregnancies, and almost 7 million hospitalizations each year in developing countries.
Why this is critical

- Frequent stockouts are common in family planning supply chains, especially in developing countries, significantly impacting public health outcomes.
- During my recent field visit to Ethiopia, stockouts were repeatedly identified by demand planners as a major barrier to effective contraceptive supply management.
- Traditional forecasting methods fail under censorship.
- Prior research inadequately addresses demand estimation under conditions of frequent stockouts and interruptions, often leading to biased forecasts and suboptimal inventory decisions.
THE FUNDEMENTAL QUESTION
Key definitions
Stockouts: Periods when demand is higher than available inventory, leading to censored observations of demand.Interruptions: Periods when no products are issued despite available stock, thus artificially recorded as zero demand.Censored Demand: Demand occurring during periods when products are unavailable (stockouts or interruptions), thus not fully observable.True Demand: Actual demand that would have occurred if sufficient stock was available or if there were no interruptions.
Censorship scenarios
How can a demand forecasting and inventory optimization model that incorporates lost sales estimation and contextual field data enhance contraceptive supply chain performance and reduce stockouts in developing countries?
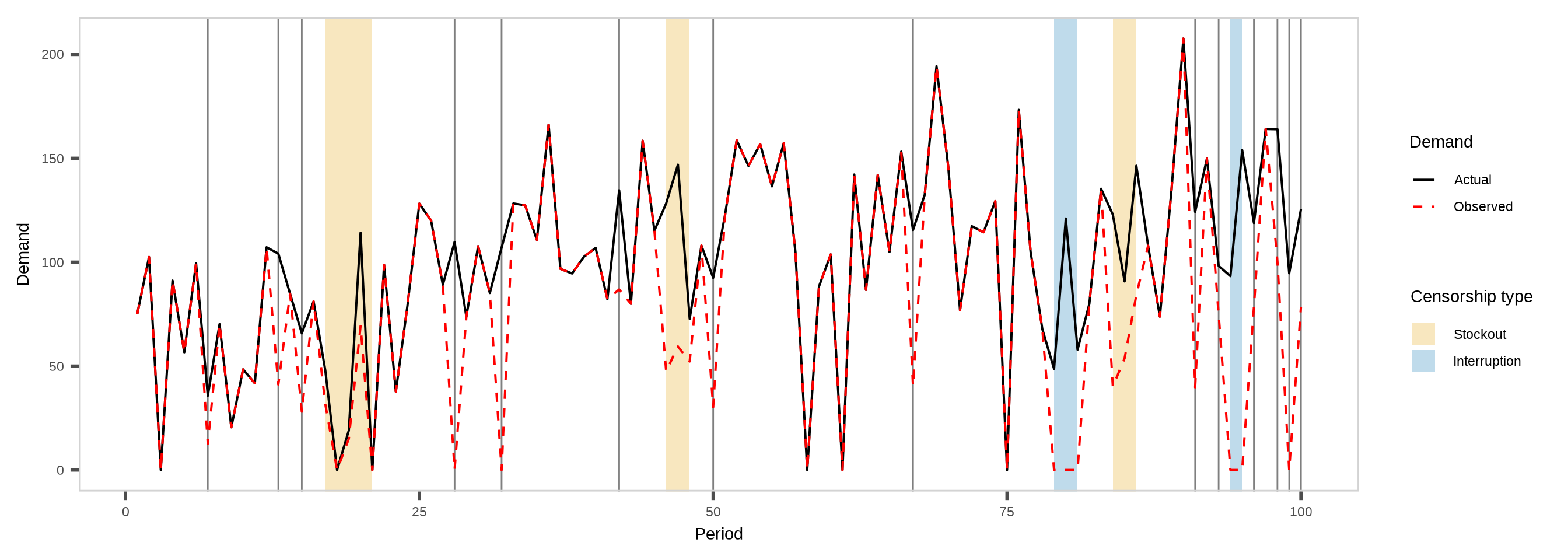
Figure 1: Censorship scenarios in family planning supply chains.
WHAT WE ARE GOING TO DO
How we can fill the gaps
- RQ1: How accurately can a Tobit Kalman Filter with conformal prediction estimate true demand under censorship?
- RQ2: How does demand reconstruction improve inventory performance compared to baseline planning methods?
- RQ3: How do planners adjust their orders in response to proposed model-generated recommendations?
Our proposed framework
First stage: Truncated Conformal Kalman Filter (TCKF)
- State-Space Formulation
\[ X_t = F X_{t-1} + \eta_t, \quad \eta_t \sim \mathcal{N}(0, Q_t) \]
- \(X_t = [\ell_t, \tau_t, \gamma_t]^T\): level, trend, seasonality
- \(F\): state transition matrix with seasonal decay and trend
- Observation Equation with Censorship
\[ y_t = \begin{cases} H X_t + \nu_t & \text{if uncensored} \\ 0 & \text{if fully censored} \\ \min(H X_t, s_t) & \text{if partially censored} \end{cases} \]
- \(H = [1, 0, 1]\): maps level and seasonality to observation
- \(s_t\): stock available at time \(t\)
First stage: Truncated Conformal Kalman Filter (TCKF)
- Kalman Prediction Step
\[ \mu_t = H \hat{X}_{t|t-1}, \quad \sigma_t^2 = H P_{t|t-1} H^T + R \]
- Censored Observation Update
\[ \hat{y}_t = \mu_t + \sigma_t \cdot \frac{\phi(z_t)}{1 - \Phi(z_t)}, \quad z_t = \frac{y_t - \mu_t}{\sigma_t} \]
\[ \hat{X}_{t|t} = \hat{X}_{t|t-1} + K_t (\hat{y}_t - \mu_t) \]
- Uses expectation of truncated Gaussian
- For fully censored (\(y_t = 0\)), skip state update; propagate uncertainty
First stage: Truncated Conformal Kalman Filter (TCKF)
- Conformal Prediction for Interval Estimation
\[ D_t \in [\max(0, \mu_t - q_\alpha), \mu_t + q_\alpha] \]
- Residuals from uncensored periods used to calibrate \(q_\alpha\)
- Ensures valid coverage without assuming normality
Note on Initialization: Initial state vector \(X_0 = [\ell_0, \tau_0, \gamma_0]^T\) is extracted via STL decomposition:
- \(\ell_0\): last STL trend
- \(\tau_0\): average slope of recent trend
- \(\gamma_0\): seasonal component or zero if undefined
- \(P_0\): diagonal matrix estimated from STL component variances
NUMERICAL EXPERIMENT
Experiment setup

Synthetic data exploration - example
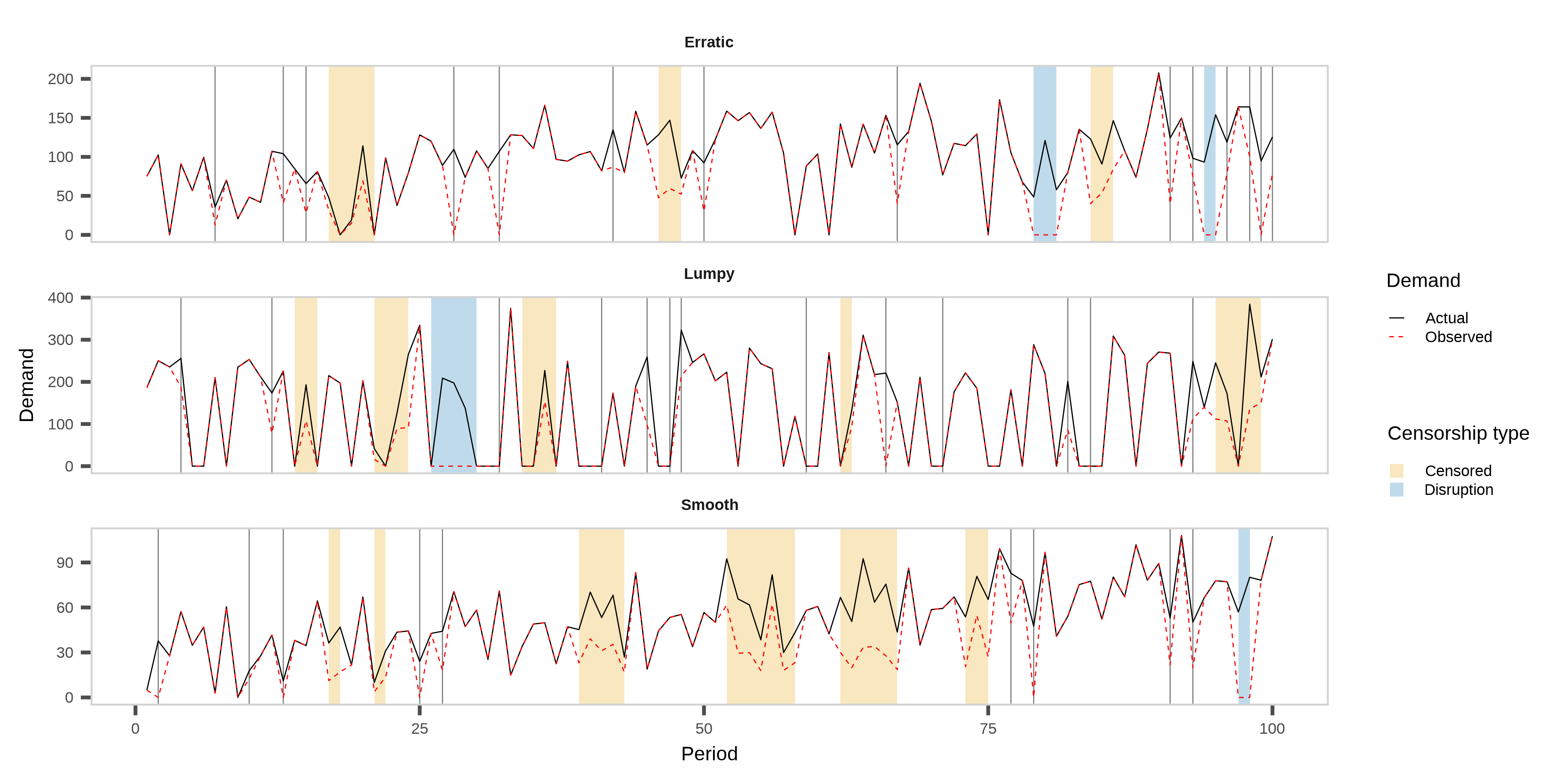
Actual vs. observed demand for one representative series per type, with disruptions and censoring shaded.
WHAT DID WE FIND
Overall forecasting and inventory performance across models
Policy 1: order-up-to level (deterministic target)
| Method | MASE (mean) | CSL (mean) | Lost Sales Rate (mean) | Inventory Efficiency (mean) | mCPR Loss (mean) |
|---|---|---|---|---|---|
| TCKF | 1.27 | 0.88 | 0.12 | 3.12 | 0.08 |
| Linear Regression | 1.52 | 0.85 | 0.14 | 2.25 | 0.1 |
| Moving Average | 1.58 | 0.83 | 0.16 | 3.69 | 0.11 |
| Naive | 1.87 | 0.86 | 0.15 | 3.22 | 0.09 |
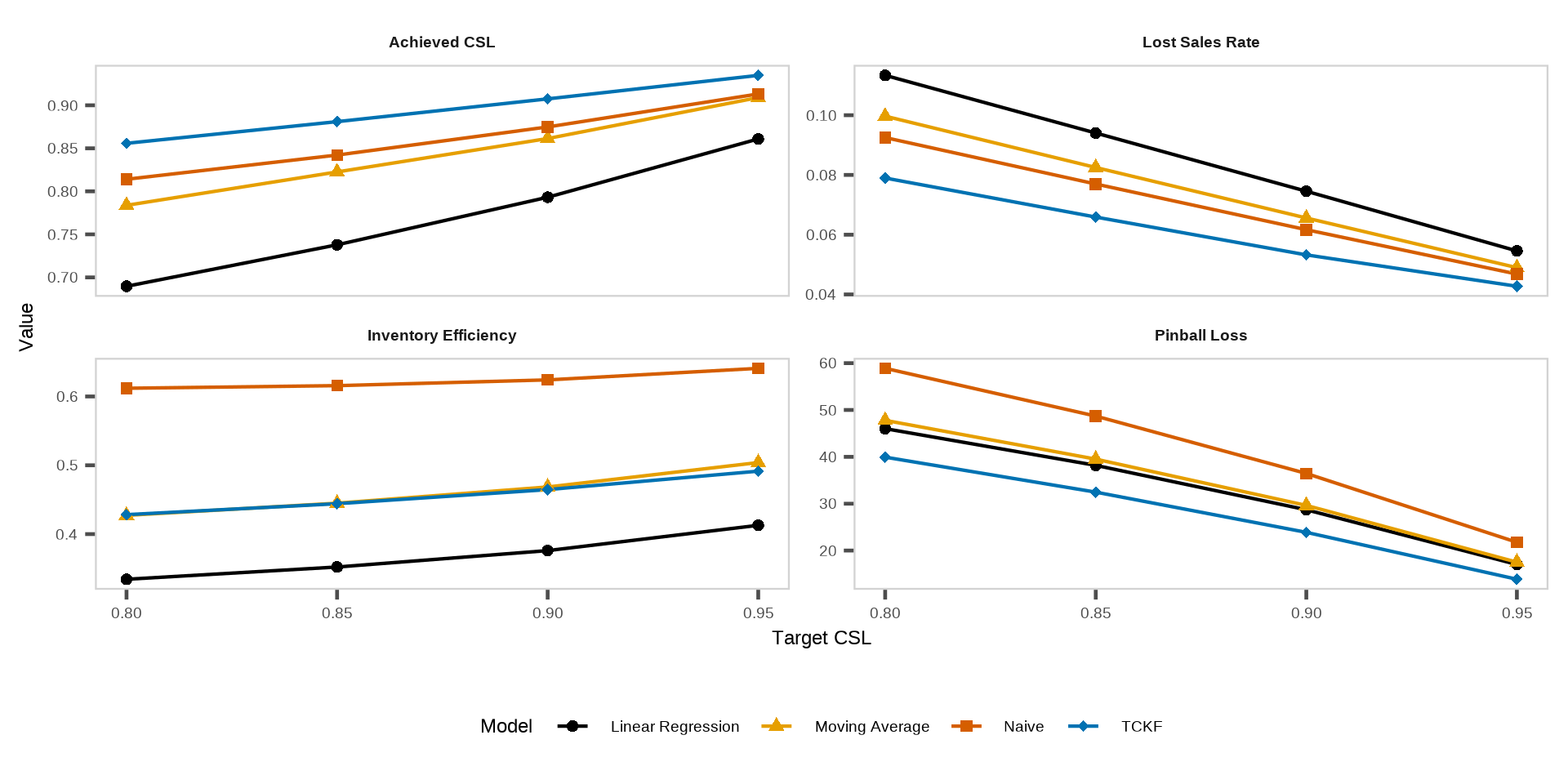
Overall forecasting and inventory performance across models
Policy 2: quantile-based order-up-to level (uncertainty-aware target) - 1 month leadtime
Public healthcare indicators across models
Policy 2: quantile-based order-up-to level (uncertainty-aware target) - 1 month leadtime
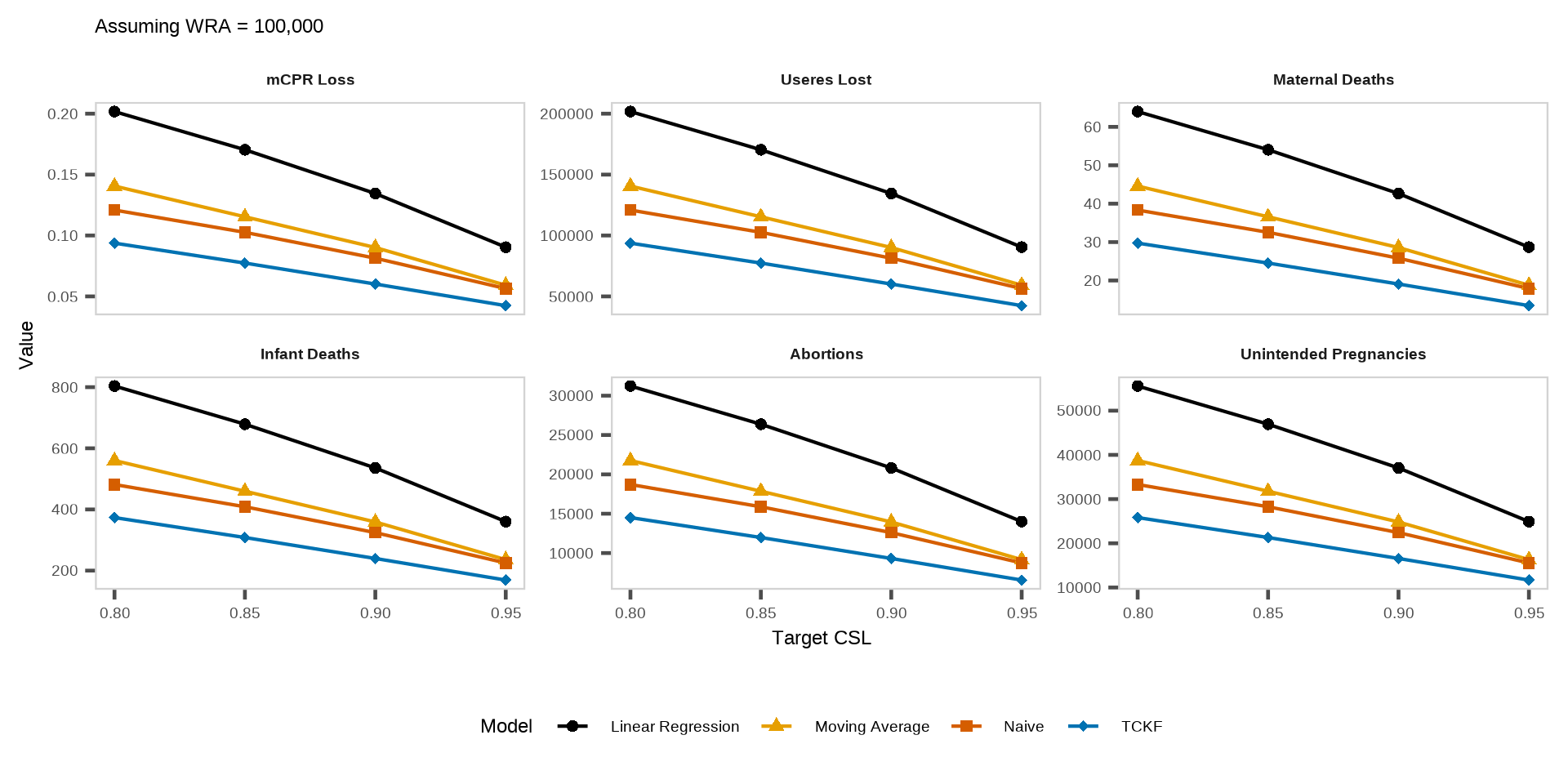
WHATS NEXT
Way forward

Add more benchmarking methods → e.g., Censored ETS,...
Extend empirical model with external covariates → Account for special events, disruptions, and policy shifts
Conduct a lab experiment with real demand planners → Measure how model recommendations affect decision-making
Any questions or thoughts? 💬

